2 Estimation de paramètre
On fixe un modèle statistique \((\mathcal{X}, \mathscr{F}, (P_\theta))\), et l’on cherche à estimer le paramètre \(\theta\) ou un autre paramètre qui dépend de \(\theta\). Dans ce chapitre, on explique comment juger la qualité d’un estimateur, et l’on donne une technique générale pour construire de bons estimateurs dans des situations assez naturelles.
2.1 Précision d’un estimateur
Définition 2.1 (Biais , risque quadratique)
- Le biais de \(\hat{\theta}\) est la quantité \(\mathbb{E}_\theta[\hat\theta - \theta]\). L’estimateur est dit sans biais s’il est de biais nul.
- Le risque quadratique de \(\hat\theta\) est la quantité \(\mathbb{E}_{\theta}[ |\hat{\theta}- \theta|^2]\).
En pratique, on peut vouloir estimer non pas \(\theta\) lui-même, mais un paramètre \(\phi = \phi(\theta)\) qui dépend de \(\theta\). Dans ce cas, si \(\hat{\phi}\) est un estimateur de \(\phi\) alors le biais est défini par \(\mathbb{E}_\theta[\hat{\phi} - \phi]\) et le risque quadratique par \(\mathbb{E}_\theta [ |\hat\phi - \phi|^2]\).
Théorème 2.1 (Décomposition biais-variance) Le risque quadratique \(\mathbb{E}_{\theta} [|\hat{\theta}-\theta|^2]\) est égal à \[ \underbrace{\operatorname{Var}_{\theta} (\hat{\theta})}_{\text{variance}} + \underbrace{\mathbb{E}_{\theta}[\hat{\theta}-\theta]^2}_{\text{carré du biais}} \, . \]
Preuve. En notant \(x\) l’espérance de \(\hat{\theta}\), on voit que le risque quadratique est égal à \(\mathbb{E}[|\hat{\theta} - x - (\theta - x)|^2]\). Le carré se développe en trois termes : le premier, \(\mathbb{E}[|\hat{\theta} - x|^2]\), est la variance de \(\hat{\theta}\). Le second, \(-2\mathbb{E}[(\hat{\theta} - x)(\theta - x)]\), est égal à \(-2(\theta - x)\mathbb{E}[\hat{\theta} - x]\), c’est-à-dire 0. Le dernier, \(\mathbb{E}[(\theta - x)^2]\), est égal à \((\theta - x)^2\), c’est-à-dire \((\theta - \mathbb{E}[\hat{\theta}])^2\) : c’est bien le carré du biais.
2.2 Convergence
La dépendance du biais ou du risque quadratique (ou d’autres indicateurs) vis à vis de la taille de l’échantillon est une question importante : pour une suite d’expériences donnée, on veut que ces indicateurs tendent vite vers zéro. Quelles sont les meilleures vitesses envisageables, et comment les obtenir ?
Rappelons brièvement deux notions de convergence des variables aléatoires. Une suite de variables aléatoires \(X_n\) à valeurs dans \(\mathbb{R}^d\) converge en probabilité vers une variable aléatoire \(X\) à valeurs dans \(\mathbb{R}^d\) si pour tout \(\varepsilon >0\), \[ \lim_{n\to\infty} \mathbb{P} (| X_n -X|> \varepsilon ) = 0. \]
On dit qu’elle converge \(\mathbb{P}\)-presque sûrement vers \(X\) si \[\mathbb{P}(\lim X_n = X) = 1.\]
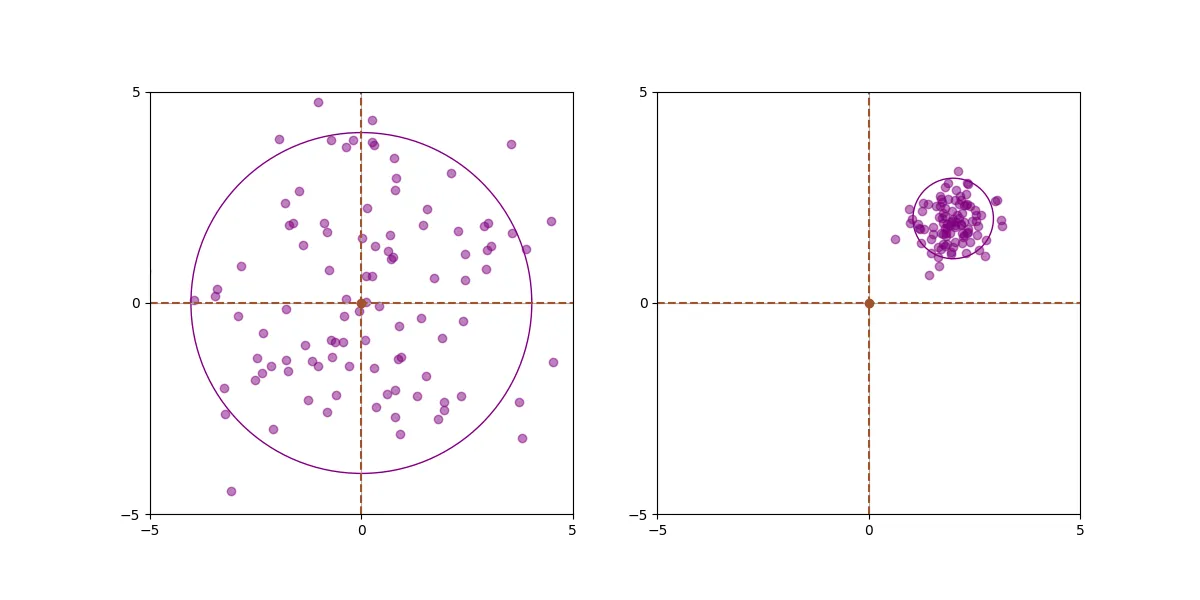
Définition 2.2 (convergence d’un estimateur) Une suite d’estimateurs \((\hat{\theta}_n)\) est convergente pour l’estimation de \(\theta\) lorsque, pour tout \(\theta \in \Theta\), sous \(P_\theta\), la suite \((\hat{\theta}_n)\) converge en probabilité vers \(\theta\) ; autrement dit, lorsque pour tout \(\varepsilon>0\), \[\lim_n P_\theta ( | \hat{\theta}_n-\theta| > \varepsilon ) =0. \] La suite est fortement convergente si, pour tout \(\theta\), la convergence a lieu \(P_\theta\)-presque sûrement.
On voit parfois le mot consistant utilisé au lieu de convergent. Je pense que c’est un anglicisme.
2.3 Normalité asymptotique
Lorsqu’un estimateur est convergent, on peut se demander à quoi ressemblent ses fluctuations autour de sa valeur limite. Le théorème central limite indique que le comportement asymptotique gaussiens est relativement fréquent, parce que beaucoup d’estimateurs sont des sommes de variables indépendantes.
Définition 2.3 (normalité asymptotique) Soit \(\theta\) un paramètre à estimer, et \(\hat{\theta}_n\) une suite d’estimateurs de \(\theta\). On dit que ces estimateurs sont asymptotiquement gaussiens (ou normaux) si, après les avoir renormalisés convenablement, ils convergent en loi vers une loi gaussienne. Autrement dit, s’il existe une suite \(a_n\) de nombres réels tels que \[ a_n(\hat{\theta}_n - \theta) \xrightarrow[n\to \infty]{\text{loi}} N(0,\Sigma)\] où \(\Sigma\) est une matrice de covariance qui dépend peut-être de \(\theta\). Pour éviter les cas dégénérés, on demande à ce que \(\Sigma\) soit non-nulle.
La normalité asymptotique sera utilisée pour construire des intervalles de confiance et des tests. Aussi, prouver que des estimateurs sont asymptotiquement normaux est une tache importante, qui est grandement simplifiée par les outils suivants.
2.4 Trois outils sur la normalité asymptotique
Vous devez maîtriser sur le bout des doigts le Théorème Central-Limite. Le Chapitre 21 de l’appendice revient sur différentes formes qu’il peut prendre.
Théorème 2.2 (Théorème Central-Limite) Soit \((X_i)\) une suite de variables aléatoires réelles, indépendantes et identiquement distribuées. On suppose que ces variables ont une variance \(\sigma^2\) finie. Alors, la variable aléatoire \[ \sqrt{n}\left(\frac{1}{n}\sum_{i=1}^n X_i - \mathbb{E}[X]\right)\] converge en loi vers une loi \(N(0,\sigma^2)\).
Un autre lemme, dit « Lemme de Slutsky », sera fréquemment utilisé pour combiner convergence en loi et convergence en probabilité.
Théorème 2.3 (Lemme de Slutsky) Soit \((X_n)\) une suite de variables aléatoire qui converge en loi vers \(X\) et \((Y_n)\) une suite de variables aléatoires qui converge en probabilité (ou en loi) vers une constante \(c\). Alors, le couple \((X_n, Y_n)\) converge en loi vers \((X,c)\) ; autrement dit, pour toute fonction continue bornée \(\varphi\), \[\mathbb{E}[\varphi(X_n, Y_n)] \to \mathbb{E}[\varphi(X,c)].\]
Preuve. Fixons une fonction test \(\varphi\) continue à support compact, donc bornée par un certain \(M\). Il faut montrer que \(\mathbb{E}[\varphi(X_n, Y_n) - \varphi(X,c)]\) tend vers zéro. L’intégrande est égal à la somme de \(A = \varphi(X_n, Y_n) - \varphi(X_n, c)\) et de \(B=\varphi(X_n, c) - \varphi(X, c)\).
Comme \(X_n\) tend en loi vers \(X\) et que \(t\to \varphi(t,c)\) est continue bornée, l’espérance de \(B\) tend vers zéro. Il faut donc montrer que l’espérance de \(A\) tend vers zéro. On fixe un \(\varepsilon>0\).
- Par le théorème de Heine, \(\varphi\) est uniformément continue : il existe \(\delta>0\) tel que \(|(x,y) - (x', y')|<\delta\) entraîne que \(|\varphi(x,y) - \varphi(x', y')|< \varepsilon/2\).
- On introduit l’événement \(\{|Y_n - c|\leqslant \delta\}\). Par le point précédent, sur cet événement on a \(|A| < \varepsilon/2\). Hors de cet événement, on peut toujours borner \(|A|\) par \(2M\). Le terme \(|\mathbb{E}A|\) est donc plus petit que \[\mathbb{P}(|Y_n - c|\leqslant \delta)\varepsilon/2 + \mathbb{P}(|Y_n - c| > \delta)2M.\]
- Comme \(Y_n\) converge en probabilité vers \(c\), lorsque \(n\) est assez grand on a \(\mathbb{P}(|Y_n - c| > \delta) < \varepsilon/4M\).
- En regroupant tout ce qui a été dit, on obtient bien \(|\mathbb{E}A| \leqslant \varepsilon\) dès que \(n\) est assez grand, ce qui montre que \(\mathbb{E}A \to 0\).
On termine par la « delta-méthode » : si une suite d’estimateurs est asymptotiquement normale, leur image par n’importe quelle fonction lisse \(g\) l’est encore, et on sait calculer la moyenne et la variance limites.
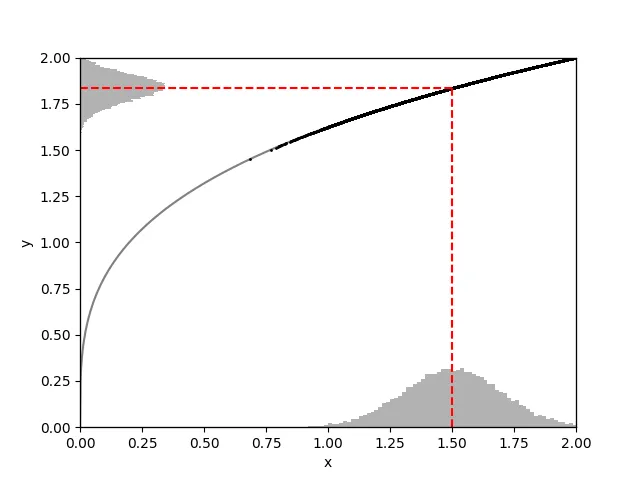
Théorème 2.4 (Delta-méthode) Soit \((X_n)\) une suite de variables aléatoires réelles telle que \(\sqrt{n}(X_n - \alpha)\) converge en loi vers \(N(0,\sigma^2)\). Pour toute fonction \(g : \mathbb{R} \to \mathbb{R}\) dérivable en \(\alpha\) (de dérivée non nulle en \(\alpha\)), alors la variable aléatoire \[ \sqrt{n}(g(X_n) - g(\alpha))\] converge en loi vers \[N(0, g'(\alpha)^2 \sigma^2).\]
Plus généralement, si les \(X_n\) sont à valeurs dans \(\mathbb{R}^d\) et que \(\sqrt{n}(X_n - \alpha) \to N(0,\Sigma)\), alors pour toute application \(g:\mathbb{R}^d \to \mathbb{R}^k\), la suite \(\sqrt{n}(g(X_n) - g(\alpha))\) converge en loi vers \[N(0, Dg(\alpha)\Sigma Dg(\alpha)^\top)\] où \(Dg(x)\) est la matrice jacobienne de \(g\) en \(x\).
Preuve. L’approximation au premier ordre de \(g\) au point \(\alpha\) dit que \(\sqrt{n}(g(X_n) - g(\alpha))\) est à peu près égale à \(\sqrt{n}(X_n - \alpha)g'(\alpha)\), et comme \(g'(\alpha)\) est une constante, ce terme converge bien en loi vers \(N(0,\sigma^2 g'(\alpha)^2)\). Il suffit donc de montrer que le terme de reste \(r_n\) qui complète le « à peu près » de la phrase précédente tend lui-même vers 0. On va montrer qu’il tend bien vers 0 en probabilité : l’application du Lemme de Slutsky ci-dessus permettra de conclure.
Soit donc \(s >0\). On veut montrer que \(\mathbb{P}(|r_n| > s)\) tend vers zéro. On se donne un \(\varepsilon >0\), et on introduit l’événement \(E_n(b) = \{|\sqrt{n}(X_n - \alpha)| < b\}\), où \(b\) est une constante arbitraire.
Par définition de la dérivabilité de \(g\) en \(\alpha\), il y a une fonction \(r\) telle que \(g(x) - g(\alpha) - (x-\alpha)g'(\alpha)\) est égal à \(r(x)\) et telle que \(r(x)/x \to 0\) quand \(x\to 0\). Au vu des définitions ci-dessus, on peut même écrire que \(r_n = \sqrt{n}r(X_n - \alpha)\). Il y a un \(\delta\) tel que si \(|x| < \delta\) alors \(|r(x)|/ |x|< s/b\).
Sur \(E_n\), dès que \(n\) est plus grand que \((b/\delta)^2\), alors \(|X_n - \alpha|<\delta\) et donc \(|r_n| < (s/b)\sqrt{n}|X_n - \alpha|\), ce qui est plus petit que \(s\). On vient de montrer que sur l’événement \(E_n\), dès que \(n\) est grand il devient impossible d’avoir \(|r_n|>s\). Par conséquent,
\[\overline{\lim}\mathbb{P}(|r_n| > s) \leqslant \overline{\lim}\mathbb{P}(\overline{E_n}).\] Or, par définition de la convergence en loi, \(\mathbb{P}(\overline{E_n})\) converge vers la probabilité \(p(b)\) qu’une variable de loi \(N(0,\sigma^2)\) soit plus grande en valeur absolue que \(b\). Cette probabilité converge vers 0 quand \(b\) est très grand, donc on peut choisir \(b\) de sorte que \(p(b)<\varepsilon\). Ainsi, \[\overline{\lim}\mathbb{P}(|r_n| > s) \leqslant \varepsilon.\] Cela entraîne bien la convergence vers 0 de \(\mathbb{P}(|r_n| > s)\).
2.5 Deux estimateurs importants
Deux estimateurs sont omniprésents en statistique : la moyenne empirique et la variance empirique. Ils sont pertinents dans n’importe quel modèle où les observations sont des réalisations de variables iid possédant une moyenne \(\mu\) et une variance \(\sigma^2\).
La moyenne empirique est définie par \[ \bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i.\] Il est évident que \(\mathbb{E}[\bar{X}_n] = \mathbb{E}[X] = \mu\). Cet estimateur est donc toujours sans biais, et son risque quadratique est égal à sa variance, c’est-à-dire \(\frac{\sigma^2}{n}\).
L’estimateur de la variance empirique est défini comme \[\hat{\sigma}_n^2 = \frac{1}{n-1}\sum_{i=1}^n(X_i - \bar{X}_n)^2.\]
Théorème 2.5 Si les \(X_i\) sont indépendants (ou simplement décorrélés), l’estimateur \(\hat{\sigma}_n^2\) est sans biais.
Preuve. Il suffit de calculer l’espérance de \((n-1)\hat{\sigma}^2_n\), ce qui revient à calculer la somme des \(\mathbb{E}[X_i^2 - 2X_i \bar{X}_n + \bar{X}_n^2]\). Il y a trois éléments dans cette expression : \(\mathbb{E}[X_i^2], -2\mathbb{E}[X_i \bar{X}_n]\) et \(\mathbb{E}[\bar{X}_n^2]\).
Le premier terme est égal à \(\sigma^2\). Le second terme vaut \(-2\sum_j \mathbb{E}[X_i X_j]/n\), et tous les termes avec \(i\neq j\) sont nuls car les \(X_k\) sont décorrélés. Il ne reste que le terme \(j=i\), à savoir \(-2 \sigma^2 / n\). Enfin, \(\mathbb{E}[\bar{X}_n^2]\) est la variance de \(\bar{X}_n\), c’est-à-dire \(\sigma^2/n\).
En additionnant tout, on obtient \(\sigma^2 - \sigma^2 / n\) et comme il y avait \(n\) termes dans la somme initiale, on obtient \((n-1)\mathbb{E}[\hat{\sigma}_n^2] = n\sigma^2 - \sigma^2\) et donc \(\mathbb{E}[\hat{\sigma}_n^2] = \sigma^2\).