$$ \newcommand{\bx}{\boldsymbol{x}} \newcommand{\bt}{\boldsymbol{\theta}} \newcommand{\bmu}{\boldsymbol{\mu}} \newcommand{\dkl}{\mathrm{d}_{\mathrm{KL}}} \newcommand{\dtv}{\mathrm{d}_{\mathrm{TV}}} \newcommand{\emv}{\hat{\theta}_{\mathrm{emv}}} \newcommand{\ent}{\mathrm{Ent}} $$

19  Test de Kolmogorov-Smirnov

On souhaite maintenant tester la distribution d’un échantillon \((x_1, \dotsc, x_n)\), c’est-à-dire tester l’hypothèse nulle : « les \(x_i\) sont des réalisations d’une variable aléatoire dont la fonction de répartition est \(F\) », où \(F\) est une fonction de répartition fixée. Le théorème de Glivenko-Cantelli dit que \(|F_n - F|_\infty\), sous l’hypothèse nulle, tend vers zéro. On rejettera donc l’hypothèse nulle si \(|F_n - F|\) est trop grand ; mais à quel seuil ?

La démonstration du théorème et l’inégalité DKW disent que la bonne échelle est \(\sqrt{n}\) : en effet, \(\mathbb{P}(|F_n - F|_\infty > \sqrt{t/n}) < 2e^{-2t^2}\). Un test dont la région de rejet est de la forme \[\left\lbrace |F_n - F|_\infty > \frac{\sqrt{\ln(2/\alpha)/2}}{\sqrt{n}}\right\rbrace\] aura un niveau de confiance plus grand que \(1-\alpha\), ce qui fournit déjà un test non-asymptotique.

En réalité, si l’on suppose seulement que \(F\) est continue, il se trouve que \(\sqrt{n}|F_n - F|_\infty\) converge en loi vers une loi connue dont on connaît les quantiles1.

Théorème 19.1 (Kolmogorov-Smirnov)  

  1. \(\sqrt{n}|F_n - F|_\infty\) converge en loi vers \(|B|_\infty\), où \((B_t)_{t\in [0,1]}\) est un pont Brownien standard2. La loi de cette variable aléatoire positive est appelée loi de Kolmogorov-Smirnov, et sa fonction de répartition \(\mathbb{P}(|B|_\infty \leqslant x)\) est donnée par \[1 - 2\sum_{k=0}^\infty (-1)^k e^{-2x^2 (k+1)^2}.\]

  2. Si \(X_1, \dotsc, X_n\) suivent une loi de fonction de répartition \(G \neq F\), alors \(\sqrt{n}|F_n - F|_\infty \to \infty\) presque sûrement.

Preuve. La démonstration du premier point nécessite des outils plus avancés en théorie des probabilités (théorème de Donsker).

Pour le second point, si \(G\neq F\), alors il existe un \(x\) tel que \(G(x) \neq F(x)\), donc \(|F(x) - G(x)|=c>0\). Or, par la loi des grands nombres, \(F_n(x)\) converge vers \(G(x)\) presque sûrement. Comme \(|F_n - F|_\infty\) est plus grand que \(|F_n(x) - G(x)|\) qui converge vers \(c>0\), on voit que dès que \(n\) est assez grand, \(\sqrt{n}|F_n - F|_\infty\) est plus grand que \(\sqrt{n}c/2\) et donc tend vers \(\infty\).

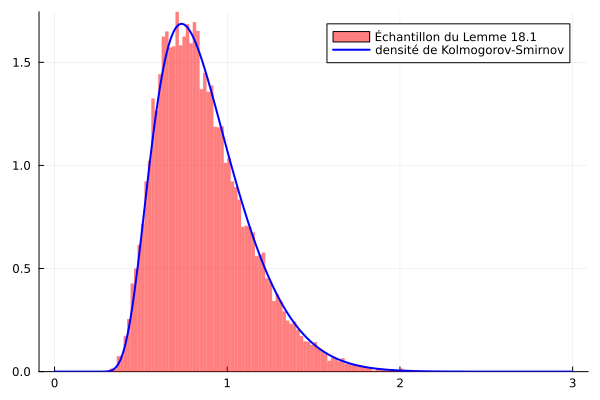
Ce théorème permet de construire des tests aymptotiques de niveau exactement \(1-\alpha\) en utilisant les quantiles de la loi de Kolmogorov-Smirnov, qui ont été tabulés. Je note \(q_\beta\) le quantile usuel, \(\mathbb{P}(\textrm{KS}< q_\beta) = \beta\). L’essentiel de la masse de cette loi est supportée sur l’intervalle \([0.5, 2]\).

\(\beta\) 0.1% 1% 95% 98% 99% 99.99%
\(q_\beta\) 0.44 0.57 1.36 1.52 1.63 2.22

  1.  La convergence en loi a toujours lieu quelle que soit la régularité de \(F\), mais en toute généralité, la limite est \(|B\circ F|_\infty\). Si \(F\) est continue, l’image de \(F\) est l’intervalle \(]0,1[\) tout entier, donc \(|B \circ F|_\infty = |B|_\infty\). Mais si \(F\) a des sauts, son image n’est pas \(]0,1[\) et donc \(|B\circ F|_\infty\) est une autre variable aléatoire, plus petite que \(|B|_\infty\).↩︎

  2. Si \(W\) est un mouvement brownien, \(B_t = W_t - tW_1\) est un pont brownien. C’est une fonction aléatoire qui vaut 0 aux points \(t=0\) et \(t=1\).↩︎