25 Densités usuelles
25.1 Lois Gamma
Une variable aléatoire de loi Gamma de paramètres \(\lambda>0, \alpha>0\) possède une densité \(\gamma_{\lambda,\alpha}(x)\) égale à \[\frac{\lambda^\alpha}{\Gamma(\alpha)}e^{-\lambda x}x^{\alpha -1}\mathbf{1}_{x>0}.\] Les lois Gamma rassemblent les lois exponentielles (\(\Gamma(\lambda, 1) = \mathscr{E}(\lambda)\)) et les lois du chi-deux qu’on verra ci-dessous \((\Gamma(1/2, n/2) = \chi_2(n)\)). La transformée de Fourier \(\varphi_{\lambda, \alpha}\) d’une loi \(\Gamma(\lambda, \alpha)\) se calcule par un changement de variables : \[\varphi_{\lambda, \alpha}(t) = \left(1 - \frac{it}{\lambda}\right)^{-\alpha}. \tag{25.1}\] Cette identité montre également que si \(X_1, \dotsc, X_n\) sont des variables indépendantes de loi \(\Gamma(\lambda, \alpha_i)\), alors leur somme est une variable de loi \(\Gamma(\lambda, \alpha_1 + \dotsc + \alpha_n)\).
25.2 Lois du chi-deux
La loi du chi-deux est la loi du carré d’une gaussienne standard \(X\). Calculons sa densité ; pour toute fonction-test \(\varphi\), \(\mathbb{E}[\varphi(X^2)]\) est donné par \[\frac{1}{\sqrt{2\pi}}\int e^{-x^2/2}\varphi(x^2)dx.\] Cette intégrale est symétrique, donc on peut ajouter un facteur 2 et intégrer sur \([0,\infty[\). En posant \(u=x^2\), on obtient alors la valeur \[ \frac{2}{\sqrt{2\pi}}\int_0^\infty e^{-u/2}\varphi(u)\frac{1}{2\sqrt{u}}du.\] On reconnaît la densité d’une loi Gamma de paramètres \((1/2, 1/2)\). Cette loi s’appelle loi du chi-deux et on la note \(\chi_2(1)\). Sa tranformée de Fourier est donnée par \[\mathbb{E}[e^{itX^2}] = \frac{1}{\sqrt{1 - 2it}}. \]
Soient maintenant \(X_1,\dotsc, X_n\) des variables de loi \(N(0,1)\) indépendantes. Chaque \(X_i^2\) est une \(\chi_2(1)\) ; leur somme a pour loi la convolée \(n\) fois de \(\chi_2(1)\). Calculons sa tranformée de Fourier : \[\begin{align}\mathbb{E}[e^{it(X_1^2 + \dotsb + X_n^2)}] &= \mathbb{E}[e^{itX_1^2}]^n \\ &= (1-2it)^{-\frac{n}{2}} .\end{align}\] On reconnaît la transformée de Fourier d’une loi \(\Gamma(1/2, n/2)\) ; cette loi s’appelle loi du chi-deux à \(n\) paramètres de liberté et elle est notée \(\chi_2(n)\). Sa densité est donnée par \[ \frac{1}{2^{n/2}\Gamma(n/2)}e^{-x/2}x^{n/2 - 1}\mathbf{1}_{x>0}. \tag{25.2}\]
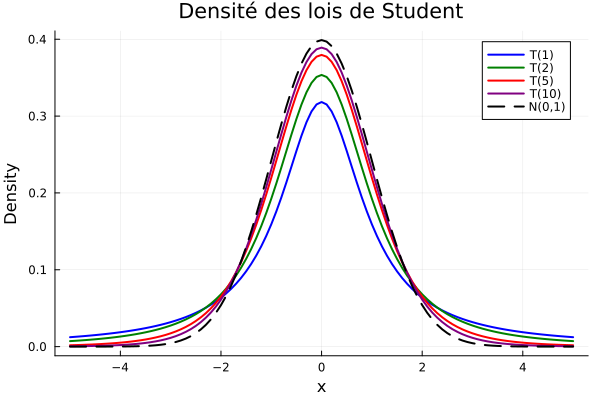
25.3 Lois de Student
Soit \(X\) une variable de loi \(N(0,1)\) et \(Y_n\) une variable de loi \(\chi_2(n)\) indépendante de \(X\). On va calculer la loi de \(T_n = X/\sqrt{Y_n/n}\). Soit \(\varphi\) une fonction test ; l’espérance \(\mathbb{E}[\varphi(T_n)]\) est égale à \[\frac{1}{Z_n\sqrt{2\pi}}\int_0^\infty \int_{-\infty}^{\infty} \varphi\left(\frac{x}{\sqrt{y/n}}\right) e^{-\frac{x^2}{2}}e^{-\frac{y}{2}}y^{\frac{n}{2} - 1}dxdy \] où \(Z_n = 2^{n/2}\Gamma(n/2)\). Dans l’intégrale en \(x\), on effectue le changement de variable \(u = x/\sqrt{y/n}\) afin d’obtenir \[\frac{1}{Z_n\sqrt{2\pi}}\int_0^\infty \int_{-\infty}^{\infty} \varphi(u) e^{-\frac{yu^2}{2n}}e^{-\frac{y}{2}}y^{\frac{n}{2} - 1}\sqrt{\frac{y}{n}} dxdy. \] La densité \(t_n(u)\) de \(T_n\) est donc donnée par \[\frac{1}{Z_n\sqrt{2\pi n}}\int_0^\infty e^{-\frac{yu^2}{2n}-\frac{y}{2}}y^{\frac{n+1}{2}-1} dy. \] Le changement de variables \(z = y(1+u^2/n)/2\) nous ramène à \[\frac{1}{Z_n\sqrt{2\pi n}}\left(\frac{2}{1+\frac{u^2}{n}}\right)^{\frac{n+1}{2}}\int_0^\infty e^{-z}z^{\frac{n+1}{2}- 1} dz.\] On reconnaît \(\Gamma((n+1)/2)\) à droite. La densité \(t_n(x)\) est donc \[t_n(x) = \frac{1}{\sqrt{n\pi}}\frac{\Gamma\left(\frac{n+1}{2}\right)}{\Gamma\left(\frac{n}{2}\right)}\left(\frac{1}{1 + \frac{x^2}{n}}\right)^{\frac{n+1}{2}}.\]
Cette loi s’appelle loi de Student de paramètre \(n\) ; on dit parfois à \(n\) degrés de liberté. Elle est notée \(\mathscr{T}(n)\). La loi de Student de paramètre \(n=1\) est tout simplement une loi de Cauchy.